最大傾斜量マップ(雪崩関連)
将来、また引っ張り出して計算するかもしれないので、そのための備忘。
最終的にはこうなった
結論から先に。斜度を国土地理院がやっている方法よりさらに良い方法を思いついたので改めて斜度計算をして地図に落とした。その結果、危険斜度があらたに浮かび上がり、より安全なトレースラインを引けた。
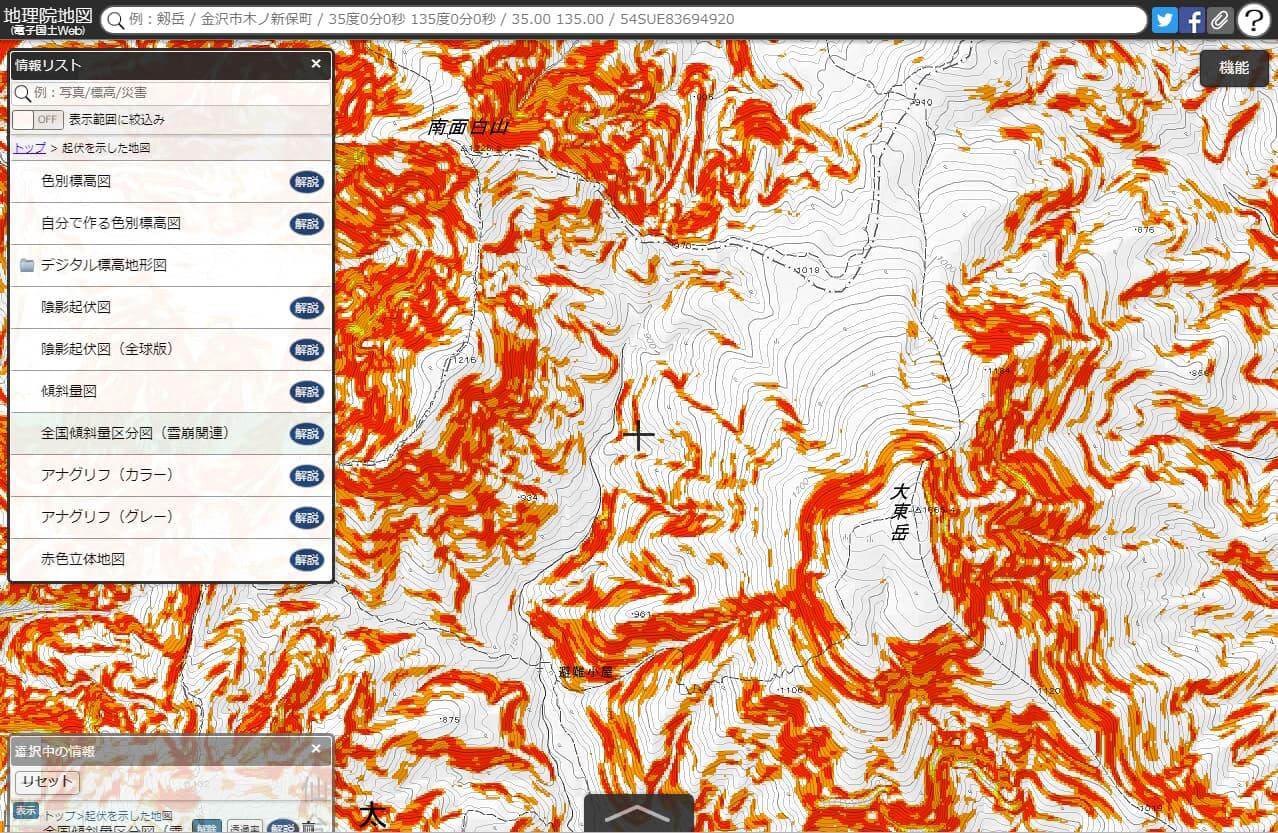
国土地理院が提供している斜度マップ。赤いのは雪崩危険地帯。
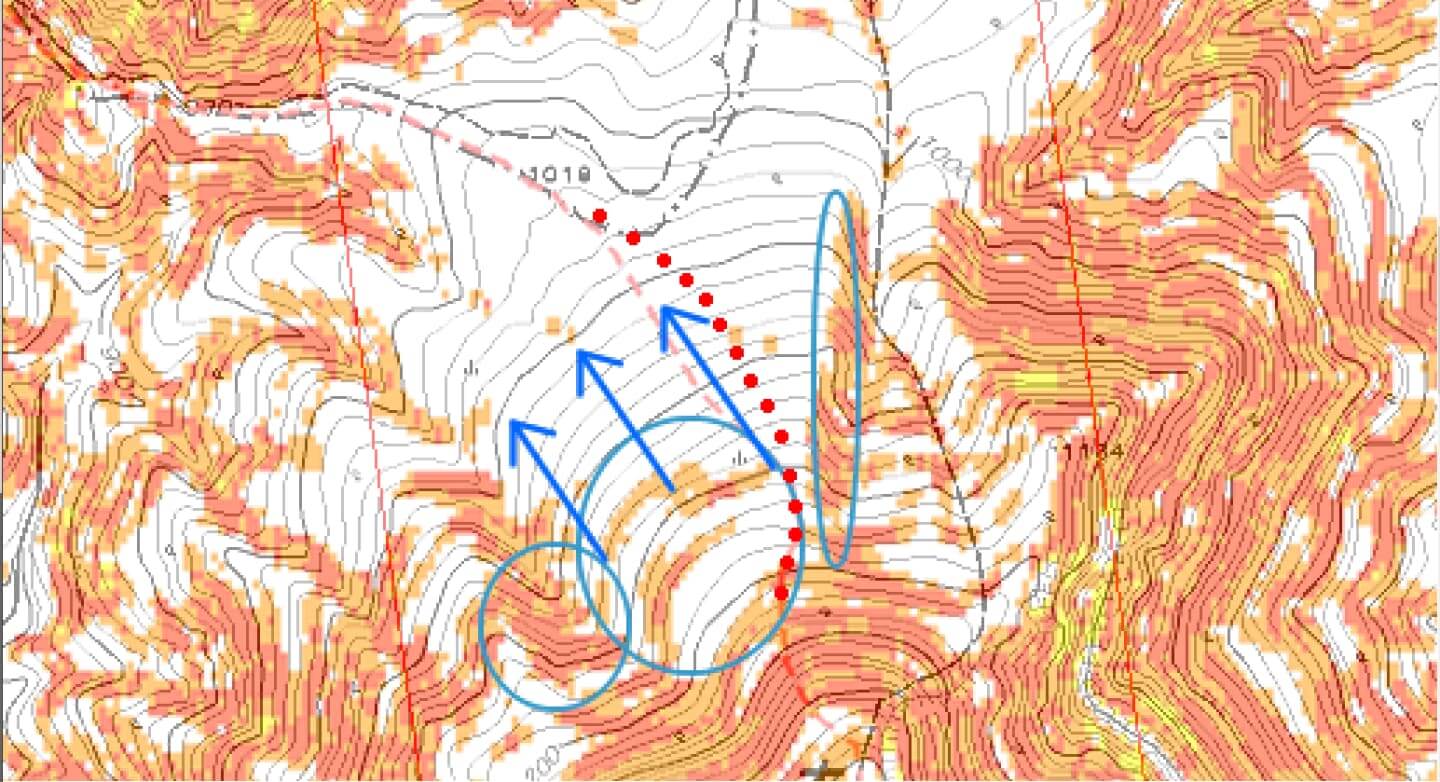
この記事の方法で得られた斜度マップ。まぁぱっとみても等高線の按配からいってこのほうが正確に見える。青い部分(例)が新たに現れた雪崩危険斜度。探せば他にもっとある。
この斜度を考慮して新たに引いたトレースライン。
何が問題で、どうやったのか
あらまし
国土地理院は既に等高線マップ(標高データ)から、斜度計算を既にしている。さらに、地理院地図に重ねるレイヤーとして提供している。しかし、国土地理院の方法は、二点ばかり欠点がある。国土地理院が算出する斜度は、提供している二次元標高分布データにおいて、ある格子点を中心に、上下6点、左右6点を使って斜度を求めている。直感的な説明をすればこうだ。南北方向、東西方向の2つの斜度を、それぞれ6点の標高データを平均することで算出。それをさらに平均した斜度を求めている。やり方としては、二乗平均の平方根を取ることで、ある中心点における代表的な斜度を定めていることとなる。各格子が、それぞれ一定(平滑)の斜面を持つとみなせる程度に格子間隔が十分に細かければそれでよいのだが、10m×10mの格子ではそうでない場所が多く見受けられる。たとえば、北東、北西、南東、南西に斜面が走っている時に、その斜面が本来持つ斜度が見えずらくなるので、危険斜度部分で鈍されて緩い斜度とみなされている部分が出てくる。また平滑した斜面を持つ1つの格子とみなして計算しているから、格子周りで斜度の向きや大きさが異なるような時、最大斜度はどっちの方向でその斜度は? という探索が重要なのだが、その点も無視されている。
ということで、この記事で求める斜度計算は4方向にそれぞれ正確な斜度を幾何学的に求めることにする。かつ、そのうちの最大斜度を採用することで斜度分布を得る。適切には、北方向、南、西、東、北東、北西、南東、南西方向の合計8方向をきちんと計算して最大斜度を求める必要がある。今回のサンプルでは東西南北に対して斜めに走った斜面で検証しているので結果は変わらない。
雪崩と傾斜度
雪崩発生のメカニズムと傾斜度の関係は比較的よく調査されている。ただし、植生の状況や、山の斜面が東西のどっちを向いているか(積雪量が全然違う)、雪崩を誘引するような特異点(突起、雪庇ができる・崩れる、落雪がおきやすい)があるか(持論)などで、事情は異なる。しかし、そういっていては定量的に推し量れない。一般的には斜度と雪崩の発生可能性の高さについてはこうされている。

国土地理院の標高データ
日本では国土地理院が、基盤地図情報数理標高モデルという標高タイルを公表しており、標高データを自由にダウンロード可能である。タイル幅は、測量方法により5m×5m(平野部、特定の火山地帯)、または、10m×10m(その他の地域)となっている。5m幅といえば、歩幅で10歩弱程度であるので、相当に精度は高い。前者は写真測量と航空レーザー測量によるもので全国は網羅していないものの、最大粗さでも10m×10m幅で国土を網羅しているということである。
国土地理院による斜度量区分マップ
国土地理院でも、上記の標高タイル(標高)を用いて全国の斜度量を算出して地図として公開している。説明資料はコチラ。
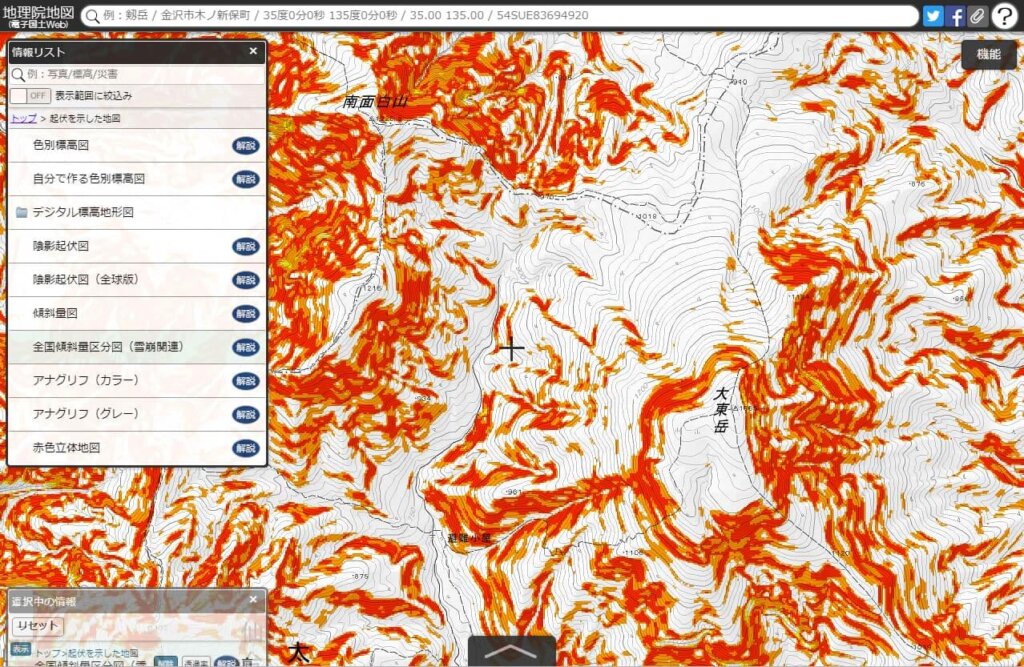
地図はコチラ。
国土地理院が採用している斜度量の欠点?
標高タイルにおける格子点8点をもちいている。直感的な説明としては、h22を中心として、東西方向のそれぞれ二方向について、南北、東西側のそれぞれ3点、合計6点を用いて、Sx、Syを算出している。これをもとにSを、二乗平均平方根S、として斜度量としている。このSの逆正接を求めることに寄って、斜度D(角度)を求めている。
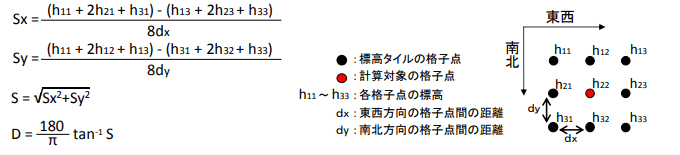
これにより上の地図を得ているのだが、2点ほど問題があるようにみえる。欠点1:h22を中心に合計8点を用いて、東西、南北というxy平面の2方向に分解してそれぞれの斜度を出しているため(ことになるので)、北西、北東、南西、南東方向に斜面が走っている場合にずれが大きいだろう(鈍る)。欠点2:そのメッシュにおける最大斜度こそが重要であるにも関わらず、合計8点に捜索範囲を広げ、二乗平均の平方根を取ってしまっているため、より簡便に滑らかに表現は出来るものの、結果的には、特異的な場所について斜度を丸めて捨てることとなる。
格子点における最大斜度を活かす方法
ぱっと思いつく単純な方法は、h22を中心として、東西南北のそれぞれ4点を用いて、三角関数(逆正接)でそれぞれの方向の斜度が分かるので、4方向のうち最大の斜度のものを使用すればよい。これにより欠点2:は克服できるが、欠点1:は残る。斜度を東西南北の2方向で定義してしまっているので、下のような地形に格子点があるときに斜度を正確に表現できていない。実際、これにより計算した場合には、本来の斜度よりゆるい斜度が算出されてしまう。たとえば、その地点における最大斜度は、北西方向に30°であったとしても、この計算では西方向に26°、といった具合となる。国土地理院が採用している、格子8点を用いた二乗平均平方根の手法も同様の傾向がでる。
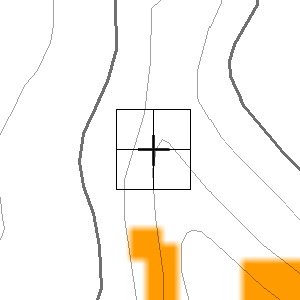
上の橙の四角のブロックは画像の関係で少し滲んでいるが、1つ1つが、まさに10m幅の格子である。等高線の間隔に比べて十分に小さいとは言えない。よって上に示したような格子に置いて斜度を求める時に、国土地理院が採用している代表斜度を求める手法では、正確に斜度を得られないことは視覚的に分かろう。
幾何学的に角度を求める
空間上の3点の格子点を通る平面と地平との成す角度を求めることで欠点1はクリアできる。たとえば、h22を中心として h12, h21を通るXYZ平面と地平面(水平面)との成す角度(斜度)を求めることとなる。h22を中心にこのようにして、3点をとっていくと、h22を中心に格子点を合計9点つかうならば、8通り(変則的な取り方をすればもう少し可能。最大84通り)の平面を規定できるが、ここでは簡易的に国土地理院との違いを明確に出すためにも、上記例の取り方で4通りで行う、つまり斜め。正しくは最低でも8通りで行うべし。すなわち、xの正負の方向, yの正負の方向で4つ、x軸, y軸と45度の方向に4方向。すなわち8方向となる。
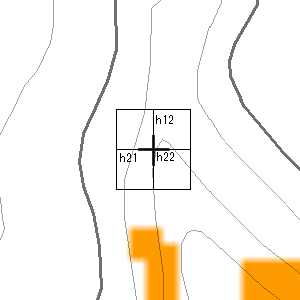
ところで、こんな平面を使わずともh22の左上h11の格子点を使えば、二点間の格子点により逆正接で簡単に左上方向の斜度は出せる。実際やってみたが、これで斜度を出すと極端なケースが多すぎて斜度の分散が大きくなりすぎるようだ。よって上の方法を採用するに至った。ということである程度はこの方法でも鈍らせている。けれど上図を見ても視覚的にはその方が正しかろうことは分かる。二乗平均平方根と二点間斜度の間に位置する方法と考えてもらえばいいのではないかと。
平面と平面の成す角
(x , y, z) 空間において、平面a1x + b1y + c1z +d1 =0、a2x + b2y + c2z +d2 =0 があるとき、この2平面のの成す角は、それぞれの平面の法線ベクトルは (a1, b1, c1)、(a2, b2, c2)であるから、cosθ = | a1a2 + b1b2 + c1c2 | / [√(a12 + b12 + c12) √(a22 + b22 + c22) ] で定義される。よって θ = cos-1 [ | a1a2 + b1b2 + c1c2 | / [√(a12 + b12 + c12) √(a22 + b22 + c22) ] ] (式1)
現在考えている一方の平面は、地平であるため、この片方の平面は z=0 となる。つまり、a1=b1=d1=0, c1=1(任意)
もう一方の平面は、h22を中心に、あと2点を選ぶこととなるが、h22は便宜的に 原点(0,0)とするとプログラム上のコーディングと計算が容易となる。他二点を選んだ時に、便宜的に中心点を0, 他を1, 2と名前をつけ、法線ベクトル (a2/d2, b2/d2, c2/d2) なる平面2を、改めて、(a2, b2, c2)により定義してから説明する。また、選んだ2点、それぞれのz値を, z0 , z1 , z2 とすれば、原点を通ることから、c2 z0 + 1 = 0となる。整理すると, z0 a2x+ z0 b2y + -z + z0= 0となる。格子間隔10(m)と、 z1 , z2 を代入して、a2, = (z1 – z0)/10z0、b2 = (z2 – z0)/10z0 と求まる。ここで求まった法線ベクトルはすべて分母にz0を有するので、全てにz0を掛けて、あらためてこれを法線ベクトル(a2, b2, c2)とする。z0、z1、z2は、地理院地図におけるそれぞれの標高データであるから、これを(式1)に代入することで斜度θが求まる。この計算をh22を中心に、n 通り (n=最小4, 適当なのは8, 最大で84=9C3=9P3/3!)行い、Max ( θn )が格子点h22における最大の斜度、最大の傾斜角となる。
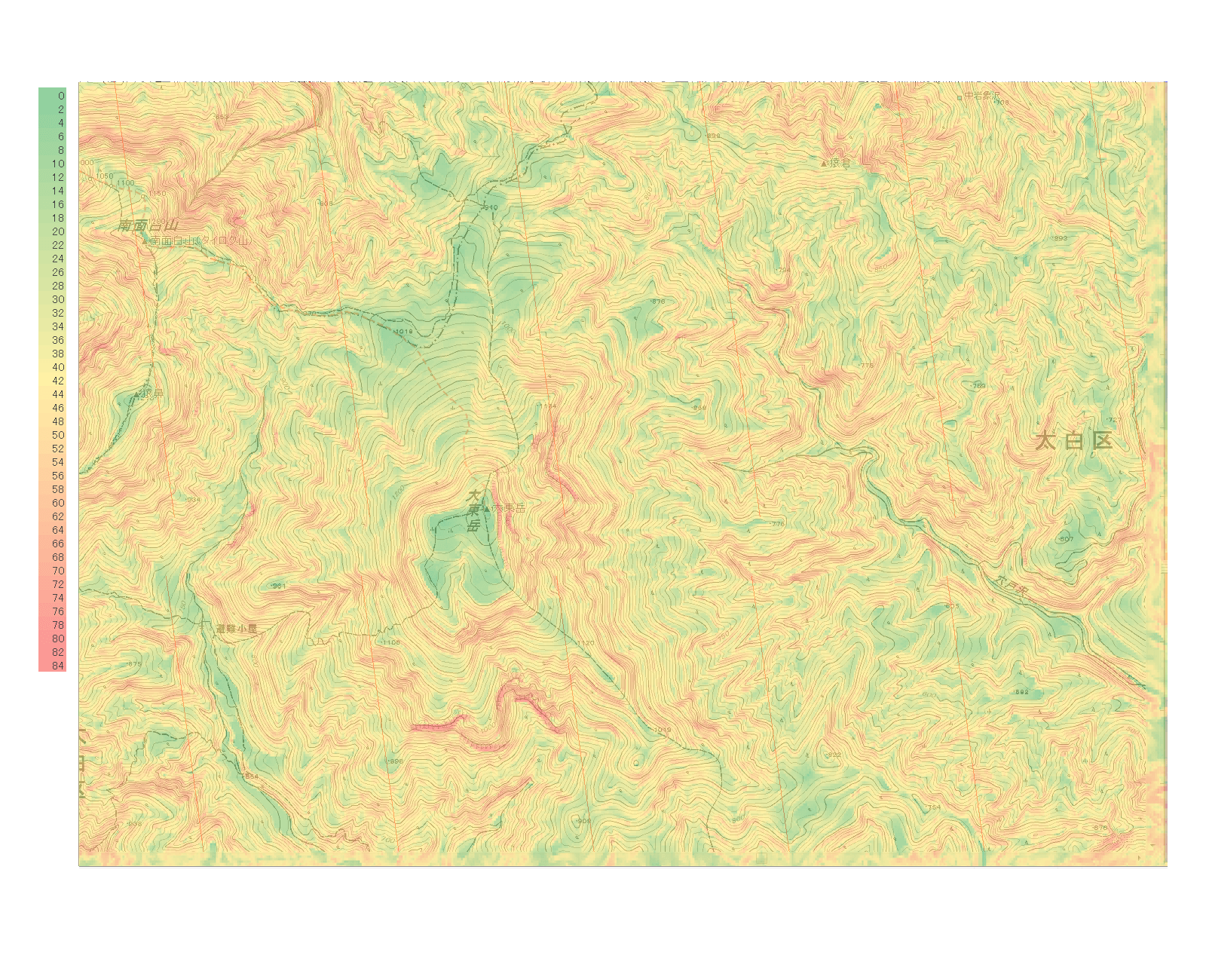
傾斜度マップ(グラデーション、原図)
上記計算により求まった傾斜度マップ。
段階的斜度区分で示した雪崩危険斜度マップ
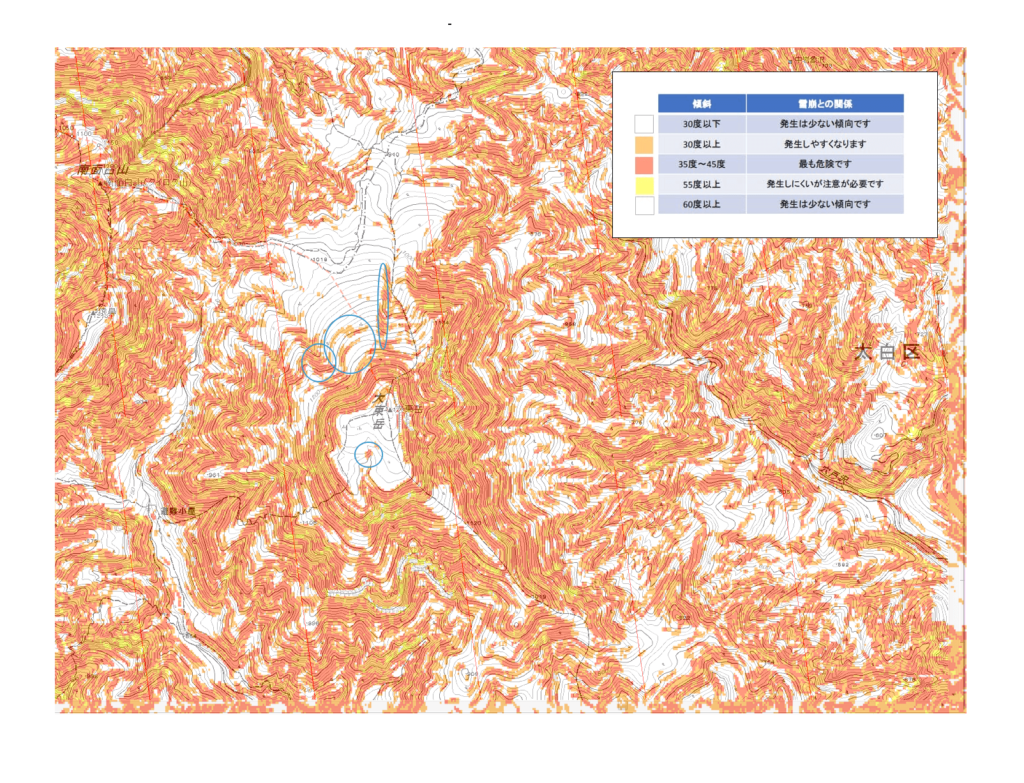
注)45°~55°も橙色としている。新たに出現した危険斜度でパッと目についた場所だけ、青く丸印をつけた。
国土地理院による同マップは下図。地理院地図が提供している斜度マップでは現れていない雪崩危険斜度が上図で現れている。大東岳山頂周りでも簡単に違いが分かる。
新たに引かれる予定トラック
数十mほど東へ寄ったほうがよさそうだ
VBA ソースコード
※色塗りがそのまま可能なのでVBAを使っているが計算は遅い。メモリ16GB、Core i7 (二年前のレベル)で数分かかる、描画が同時におこると極めて遅くなるため、Run前はすべてのセルを無色にして、条件付き書式等は一旦すべて解除するべし。計算するだけならfortranがベター。ただし、格子点、標高をきちんと別ファイルに作る必要があるのでその手間はかかる。日本全土を計算するならば当然その方法で。ちゃんとした解析屋さんがみればまず倍精度じゃないからだめだ!とか叱られそうだが!
Sub eve()
ii = 3
For j = 0 To 749
For i = 0 To 1124
ii = ii + 1
Cells(j + 3, i + 3) = Cells(ii, 1)
Next
Next
End Sub
Sub gradient2()
‘3次元平面と水平面の成す角を求め、最大斜度を決定する。(4通り)
‘必要に応じて12通り
For j = 4 To 1126 ‘1126 ‘1126 ‘列
For i = 5 To 751 ‘751 ‘行
g5 = 0
‘右上
‘ (0,0,1) ( cells(i-1,j)/10, cells(i,j+1)/10, -1)
cos1 = 1 / Sqr(((Cells(i – 1, j) – Cells(i, j)) / 10) ^ 2 + ((Cells(i, j + 1) – Cells(i, j)) / 10) ^ 2 + 1)
rad = ACN(cos1)
g1 = GetAngle(rad)
cos2 = 1 / Sqr(((Cells(i – 1, j) – Cells(i, j)) / 10) ^ 2 + ((Cells(i, j – 1) – Cells(i, j)) / 10) ^ 2 + 1)
rad = ACN(cos2)
g2 = GetAngle(rad)
cos3 = 1 / Sqr(((Cells(i + 1, j) – Cells(i, j)) / 10) ^ 2 + ((Cells(i, j + 1) – Cells(i, j)) / 10) ^ 2 + 1)
rad = ACN(cos3)
g3 = GetAngle(rad)
cos4 = 1 / Sqr(((Cells(i + 1, j) – Cells(i, j)) / 10) ^ 2 + ((Cells(i, j – 1) – Cells(i, j)) / 10) ^ 2 + 1)
rad = ACN(cos4)
g4 = GetAngle(rad)
h = Application.WorksheetFunction.Max(g1, g2, g3, g4)
If h < 30 Then
‘h = 0
Cells(755 + i, j).Interior.Color = RGB(255, 255, 255)
End If
If h >= 30 And h < 35 Then
‘ h = 1
Cells(755 + i, j).Interior.Color = RGB(255, 153, 0)
End If
If h >= 35 And h < 45 Then
‘ h = 2
Cells(755 + i, j).Interior.Color = RGB(255, 51, 0)
End If
If h >= 45 And h < 55 Then
‘h = 3
Cells(755 + i, j).Interior.Color = RGB(255, 153, 0)
End If
If h >= 55 And h < 60 Then
‘h = 3
Cells(755 + i, j).Interior.Color = RGB(255, 255, 0)
End If
If h >= 60 Then
‘h = 4
Cells(755 + i, j).Interior.Color = RGB(255, 255, 255)
End If
‘Cells(755 + i, j) = Round(h, 1)
‘Debug.Print cos1, cos2, cos3, cos4
‘If g6 < h Then
‘ g6 = g5
‘End If
Next
Next
‘Debug.Print g6
‘125% 162% on fireworks
End Sub
Function ACN(x) ‘逆余弦 arccos
Select Case x
Case Is = -1
ACN = pi
Case Is = 1
ACN = 0
Case Else
ACN = pi / 2 – Atn(x / Sqr(1 – x ^ 2))
End Select
End Function
Function pi()
pi = Atn(1) * 4
End Function
Function GetRadian(ByVal angle)
GetRadian = angle * (pi / 180)
End Function
Function GetAngle(ByVal radian)
GetAngle = radian / (pi / 180)
End Function